从简单的case讲算法优化--斐波那契数列

数学背景

公元1150年印度数学家 Gopala和金月在研究箱子包装对象长宽刚好为1和2的可行方法数目时，首先描述这个数列。在西方，最先研究这个数列的人是比萨的列奥那多（意大利人斐波那契Leonardo Fibonacci），他描述兔子生长的数目时用上了这数列:

兔子对的数量就是斐波那契数列

第一个月初有一对刚诞生的兔子

第二个月之后（第三个月初）它们可以生育

每月每对可生育的兔子会诞生下一对新兔子

兔子永不死去

当我们了解斐波那契数列的定义以后，我们通过列举的方式可以得出如下的表格：

月份	兔子数(对)
1个月	1
2个月	1
3个月	2
4个月	3
5个月	5
6个月	8
7个月	13
…	…
n个月	F(n)

其实，通过观察，我们很容易能够找出一个规律：

当月的兔子对数 = 上个月的兔子总对数 + 截至上月为止已经成熟的可生育的兔子对数

(因为每个月每一对成熟的兔子都会产下1对新兔子)

通过观察上面的表格规律，或者说做一些简单的数学推论，其实很显然就可以得到斐波那契数列数学意义上的递推关系：

if n == 1, then F(n) = 1;

if n == 2, then F(n) = 1;

if n > 2, then F(n) = F(n - 1) + F(n - 2);

递归，自顶向下(recursion)

了解了斐波那契数列相关的数学背景后,其实我们就可以着手去解决这个问题了。从斐波那契数列的递推公式中，我们很容易看出斐波那契数列采用递归的方式去解是比较直观的。

const fabonacci = (n) => {
  if(n === 1 || n === 2) return 1;
  return fabonacci(n - 1) + fabonacci(n - 2);
}

嗯，第一版最low的斐波那契数列算是完成了，感觉也不是很难理解，基本上就是对于斐波那契数列递推式的一个代码翻译。从功能上来说，这个斐波那契数列确实是已经完成了，至于负数甚至小数的输入校验我们暂且不去考虑他，我们先来看看一个实际运行中的问题。

1	fabonacci(100)

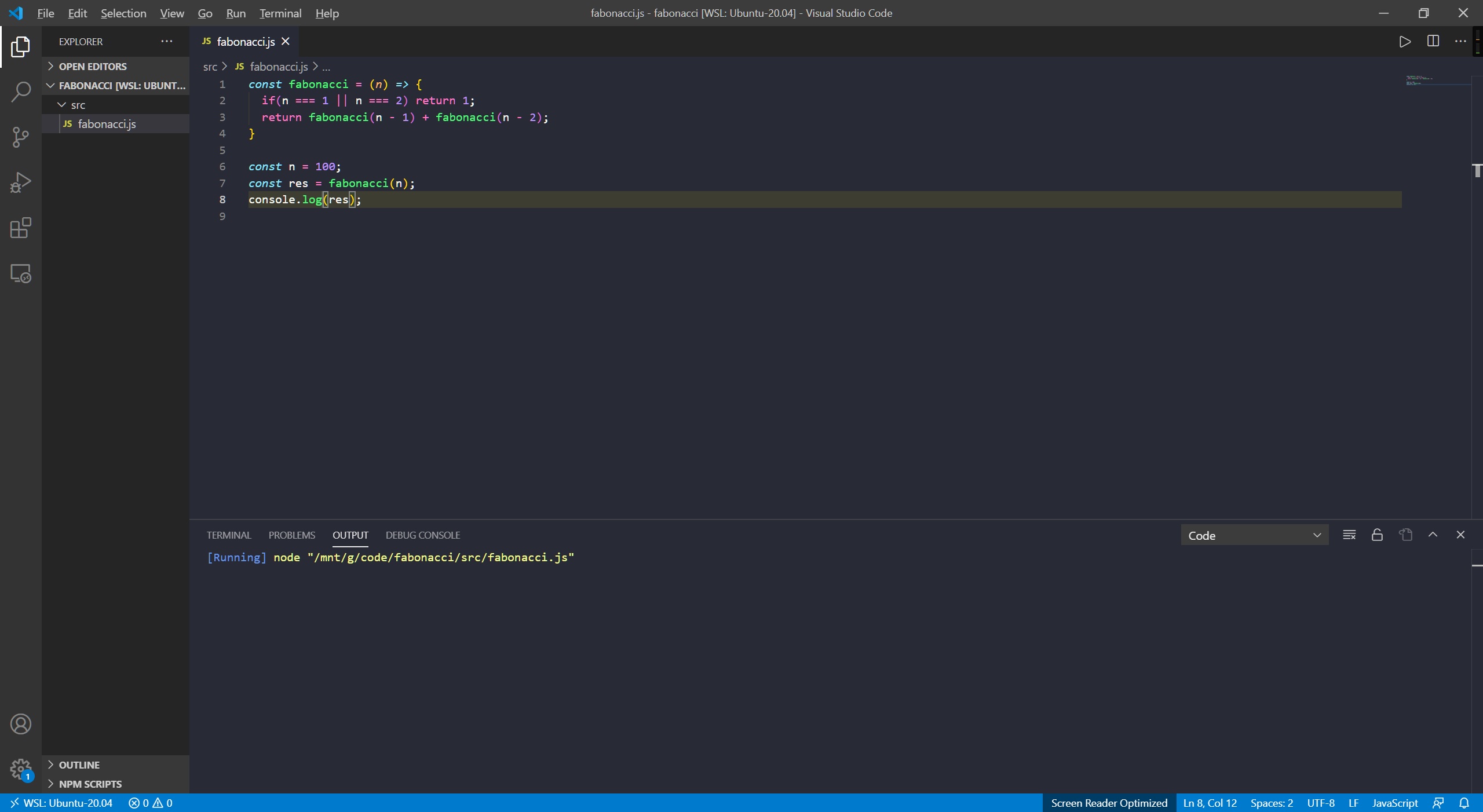
我们发现在node环境中实际运行算法计算第100项的时候程序直接挂起了，出不来结果。当然另外需要注意的是由于斐波那契数列第100项的数值太大了，通过js计算出来的结果会有数值溢出问题，关于js大整数的点我们暂且也不去考虑。

其实我们的计算出不来结果，是因为我们用递归写的算法性能太差了，其中主要有两方面的问题：

函数调用栈问题，容易出现stack overflow，也就是我们说的爆栈

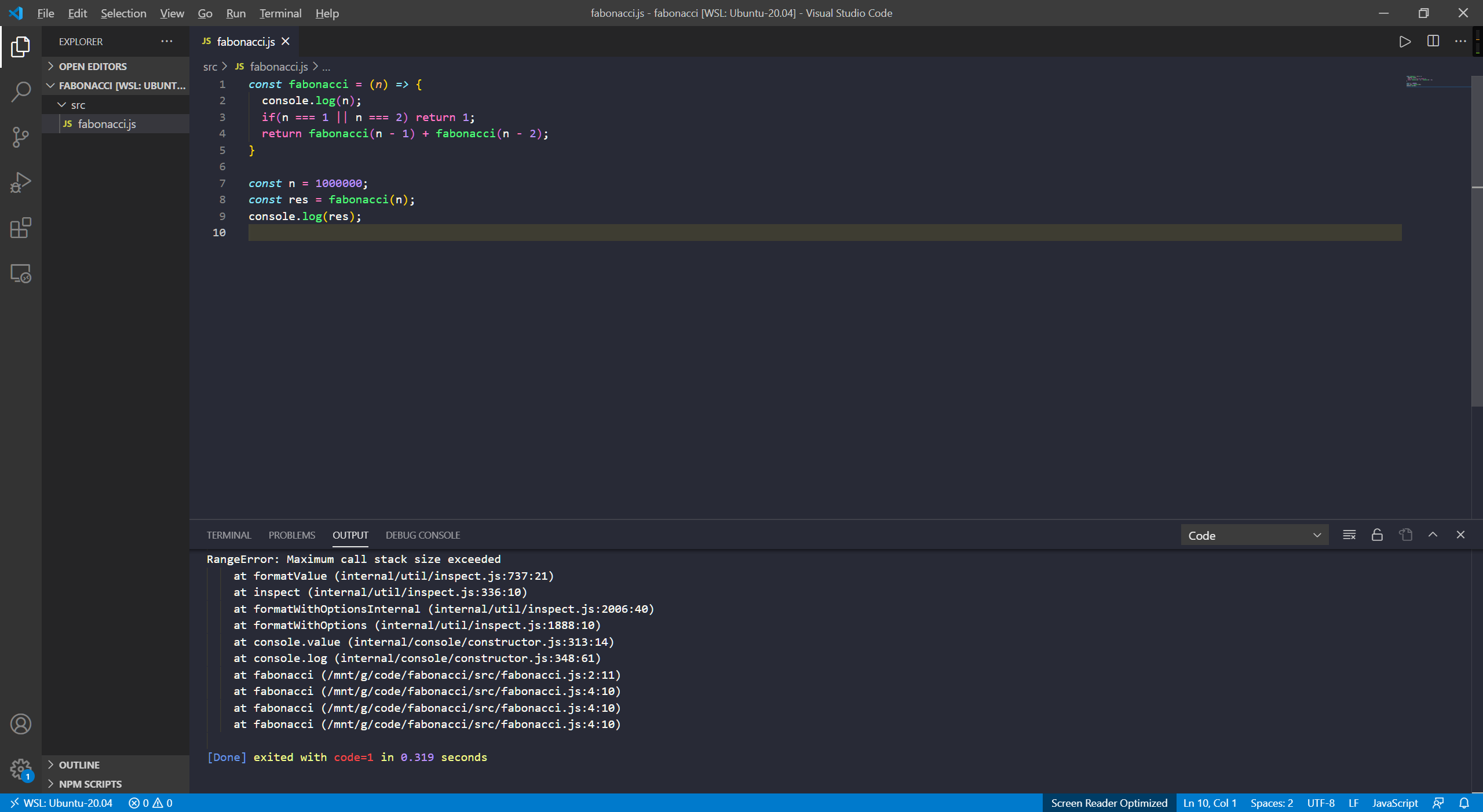
我们先从f(5)说起

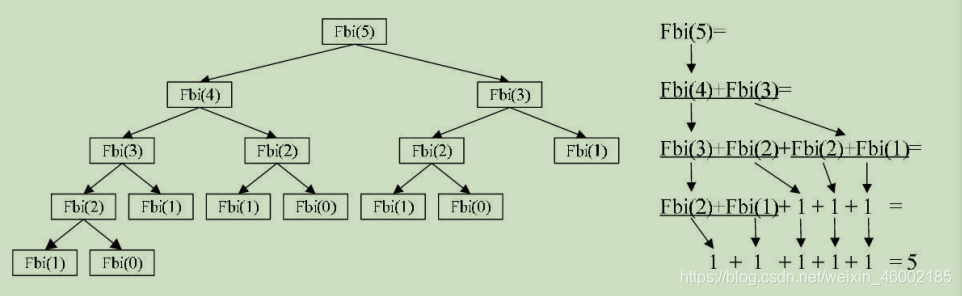
很显然，我们每次从堆栈中想要计算f(n)时，必须先计算f(n - 1)和f(n - 2)，此时无法得出f(n)的值，因此f(n)的运行环境必须保存在函数调用栈中，当计算的n值过大时就会导致栈溢出
函数重复计算问题，大部分的重复计算浪费计算性能

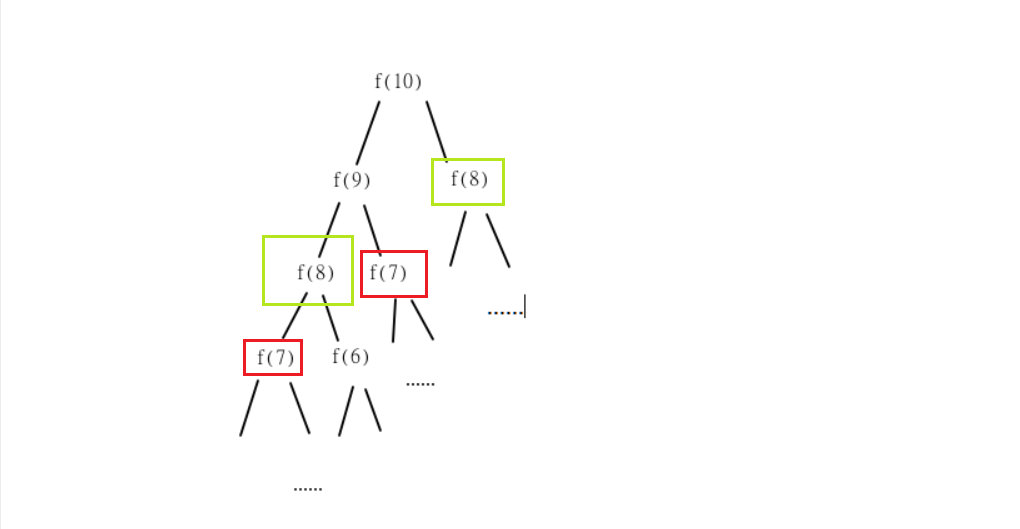
在计算f(10)的过程中，f(9)计算1次，f(8)计算2次，f(7)计算3次，f(6)计算5次……

假设F(n)表示重复计算f(n)的次数，很显然得到的式子类似于斐波那契数列

if n == input, then F(n) = 1;

if n == input - 1, then F(n) = 1;

if n < input - 2, then F(n - 2) = F(n - 1) + F(n );

(因为要计算f(n) 和f(n - 1)必须先计算f(n - 2)，所以很显然f(n - 2)的计算次数等于f(n - 1) 和f(n)的计算次数之和)

递归优化(optimize)

知道斐波那契数列的递归计算存在问题，我们需要考虑对于当前算法进行优化

尾递归

对于函数调用栈的优化，我们可以考虑使用尾递归优化。

只是目前关于尾递归，除了safari的浏览器(仅严格模式下有效)，其余浏览器均不支持尾递归优化，因此目前尾递归的优化暂时是无效的，期待后续各大浏览器都能支持上尾递归优化。

checklist: 各大浏览器对于es6支持

尾调用

尾递归：一个函数在最后返回函数自身的调用
$$
尾递归 = 尾调用 + 递归
$$

只有不再调用到外层函数的内部变量，内层函数的调用帧才会取代外层函数的调用帧，否则就无法进行“尾递归调用”

(原文出自《ES6标准入门（第三版）》，阮一峰著)

尾递归优化的本质是让函数内层递归调用帧取代外层调用帧，函数调用栈中永远只保留一个调用帧，因此也就能够避免栈溢出的问题了。

const fabonacci = (n) => {
  if(n === 1 || n === 2) return 1;
  return fabonacci(n - 1) + fabonacci(n - 2);
}

const tailFabonacci = (n, n_2 = 1, n_1 = 1) => {
  if(n === 1 || n === 2) return n_1;
  return tailFabonacci(n - 1, n_1, n_1 + n_2);
}

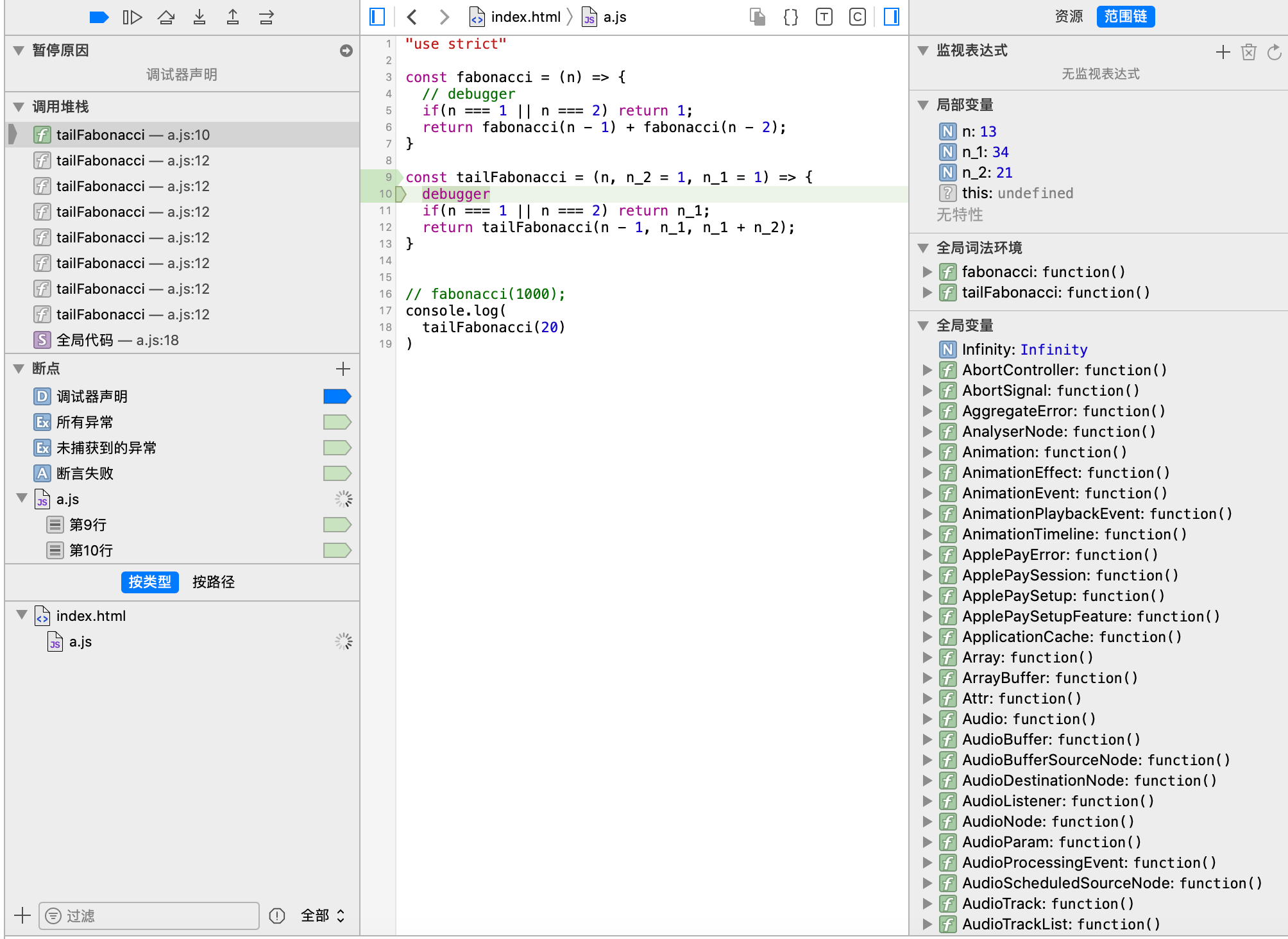
尾递归调用栈

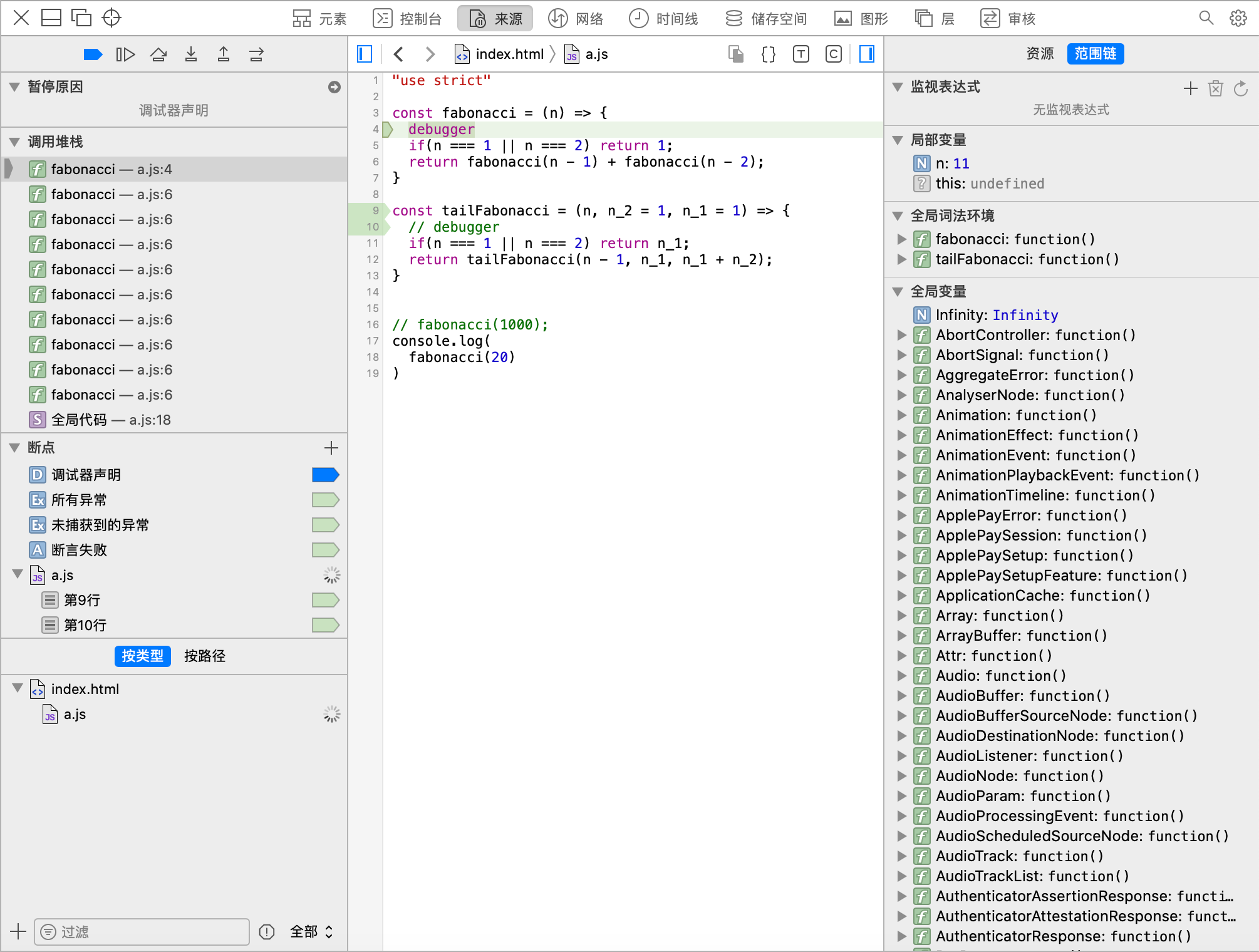
朴素递归调用栈

看一个阶乘的例子：
$$
f(n) = n * f(n - 1) (n > 1) \\
f(n) = 1 (n === 1)
$$

// 朴素递归
const factorial = (n) => {
  if (n === 1) return 1;
  return n * factorial(n - 1);
}

// 尾递归
const tailFactorial = (n, multy = 1) => {
  if (n === 1) return multy;
  return tailFactorial(n - 1, n * multy);
}

记忆化搜索

记忆化的方法本质上是根据函数参数设置相应的缓存，利用函数的参数进行hash运算。当函数运行时，命中缓存后，可以直接从缓存中读取计算结果，而不需要重新计算。缓存对于一些经常性进行的高CPU消耗的计算有比较大的作用。

使用缓存需满足函数必须保证为纯函数，无副作用

const memoize = (fn) => {
  const _cache = {};
  return (...args) => {
    const hash = JSON.stringify(args);
    if(!_cache[hash]) {
      _cache[hash] = fn(...args);
    }
    return _cache[hash];
  }
}

const fabonacci = memoize((n) => {
  if(n === 1 || n === 2) return 1;
  return fabonacci(n - 1) + fabonacci(n - 2);
})

/**
容易出现问题的写法：
fabonacci引用问题，只有第一次调用函数时，走了缓存
后面fabonacci的调用走具名函数

const fabonacci = (n) => {
	if(n === 1 || n === 2) return 1;
	return fabonacci(n - 1) + fabonacci(n - 2);
}
const memoizeFabonacci = memoize(fabonacci);
**/

const fabonacci = (n) => {
  if (n === 1 || n === 2) return 1;
  else return fabonacci(n - 1) + fabonacci(n - 2);
}

const fakerMemoFab = memoize(fabonacci);

console.log(
  timer(fabonacci, [43], console.log)
)

console.log(
  timer(fakerMemoFab, [43], console.log)
)

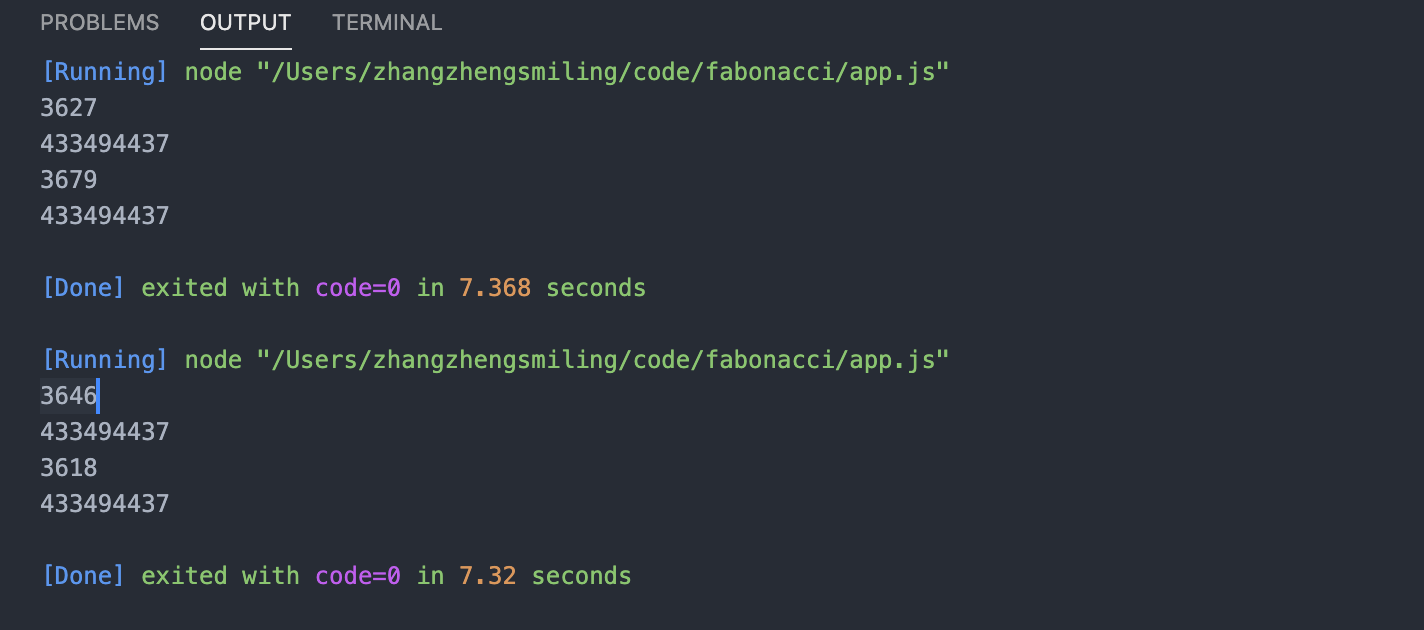
迭代，自底向上(Iterator)

动态规划的思想

问：一层楼梯上共有20级阶梯，一次可以选择上1级或者2级，总共有多少种方法？

思考逻辑：

每次只能上1级或者2级楼梯，因此如果要到达第20级，那么只能从第19级阶梯爬1级或者从第18级阶梯爬2级，

因此对于20级阶梯的方法数，由到达第19级的方案数 + 到达第18级的方案数

$$
dp[n] =
\begin{cases}
dp[n - 1] + dp[n - 2], & \text{if }n\text{ > 2} \\
1, & \text{if }n\text{ <= 2}
\end{cases}\\
$$

动态规划问题，思考上可以自顶向下去思考，实现上通常采用自底向上的方式
$$
dp[1] = 1;\\
dp[2] = 2;\\
dp[3] = 1 + 2 = 3;\\
dp[4] = 2 + 3 = 5\\
…
$$

问：金币收集问题

在M*N的方格内，散落了一些金币，其中单个小方格内有1个或者0个金币，由matrix[M][N]表示

一个机器人从[0, 0]位置出发，向[M-1, N-1]位置走，走的过程中可以拾取散落的金币

但是机器人只能向右或者向下走，问机器人最多能收集多少金币
$$
\begin{matrix}
0&0&0&0&1&0 \\
0&1&0&1&0&0\\
0&0&0&1&0&1\\
0&0&1&0&0&1\\
1&0&0&0&1&0
\end{matrix}
$$

$$
dp[i][j] = max \left\{ dp[i-1][j] + matrix[i][j], dp[i][j-1] + matrix[i][j] \right\}
$$

Base case: when i === 0 || j == = 0

解动态规划问题的关键：

判断问题是否满足动态规划的条件

base case

dp方程

关于动态规划问题

最优解：矩阵快速幂

快速幂

$$
pow(m, n) =
\begin{cases}
pow(m * m, n / 2), & \text{if }n\text{ is even} \\
pow(m * m, Math.floor(n / 2)) * m, & \text{if }n\text{ is odd}
\end{cases}\\
$$

在一般的逻辑下，我们求m^ n，是通过O(n)的遍历，然后对于m做累乘计算，但快速幂的思想在于将乘法次数进行了优化成了O(log n)

/**
 * 数论，快速幂
 * @param base 
 * @param n 
 * @returns 
 */
export const quickPowRecursion = (base: number, n: number): number => {
  if(n === 0) return 1; 
  if(n === 1) return base;
  if(n % 2 === 0) {
    const _temp = quickPowRecursion(base, n / 2);
    return _temp * _temp;
  } else {
    const _temp = quickPowRecursion(base, (n - 1) / 2);
    return base * _temp * _temp;
  }
}

export const quickPow = (base: number, n: number) => {
  if(n === 0) return 1;
  let res = base;
  while(n > 1) {
    if(n % 2 === 0) {
      res = res * res;
      n = n / 2;
    } else {
      res = base * res * res;
      n = (n - 1) / 2;
    }
  }
  return res;
}

矩阵快速幂

$$
\left(
\begin{matrix}
f(n & f(n - 1) \\
\end{matrix}
\right)
=
\left(
\begin{matrix}
f(n - 1) & f(n - 2) \\
\end{matrix}
\right)
*
\left(
\begin{matrix}
1 & 1 \\
1 & 0 \\
\end{matrix}
\right)
=
\left(
\begin{matrix}
f(n - 2) & f(n - 3) \\
\end{matrix}
\right)
*
\left(
\begin{matrix}
1 & 1 \\
1 & 0 \\
\end{matrix}
\right)^2
= …
$$

矩阵快速幂的优化与快速幂一致，通过将矩阵的幂运算进行优化，矩阵快速幂可以应用于一些类似递推式的计算，将O(n)的朴素算法优化成O(log n)的矩阵乘法

例如：
$$
f(n) = a * f(n - 1) + b * f(n -2) + c * f(n - 3)
$$

$$
\left(
\begin{matrix}
f(n) & f(n - 1) & f(n -2) \\
\end{matrix}
\right)
=
\left(
\begin{matrix}
f(n - 1) & f(n - 2) & f(n - 3) \
\end{matrix}
\right)
*
\left(
\begin{matrix}
a & 1 & 0 \\
b & 0 & 1 \\
c & 0 & 0
\end{matrix}
\right)
=
\left(
\begin{matrix}
f(n - 2) & f(n - 3) & f(n - 4) \\
\end{matrix}
\right)
*
\left(
\begin{matrix}
a & 1 & 0 \\
b & 0 & 1 \\
c & 0 & 0
\end{matrix}
\right)^2
= …
$$

class Matrix {
  value: number[][];
  rows: number;
  cols: number;
  constructor(rows: number, cols: number) {
    this.rows = rows;
    this.cols = cols;
    this.value = new Array(rows)
      .fill("")
      .map(item => new Array(cols).fill(0));
  }

  fill(num: number): Matrix {
    for(let i = 0; i < this.rows; i++) {
      for(let j = 0; j < this.cols; j++) {
        this.value[i][j] = num;
      }
    }
    return this;
  }

  set(nums: number[][]) {
    const r = nums.length;
    if(r !== this.rows) throw new Error('rows not matched...');
    const c = nums[0].length;
    if(c !== this.cols) throw new Error('cols not matched...');
    this.value = nums;
    return this;
  }

  multiple(matrix: Matrix) {
    if(this.cols !== matrix.rows) throw new Error('not permission...');
    const m1 = this.value;
    const m2 = matrix.value;
    const rows = this.rows;
    const cols = matrix.cols;
    const mRes = new Array(rows).fill('')
      .map(
        item => new Array(cols)
      );
    for(let i = 0; i < rows; i++) {
      for(let j = 0; j < cols; j++) {
        let res = 0;
        for(let k = 0; k < this.cols; k++) {
          res += m1[i][k] * m2[k][j];
        }
        mRes[i][j] = res;
      }
    }
    const matrixRes = new Matrix(rows, cols);
    matrixRes.set(mRes);
    return matrixRes;
  }

  fastPow(n: number): Matrix{
    const matrix: Matrix = new Matrix(
      this.rows, this.cols
    );
    matrix.set(this.value);
    if(n === 0) return matrix;
    let res: Matrix = matrix;
    while(n > 1) {
      if(n % 2 === 0) {
        res = res.multiple(res);
        n = n / 2;
      } else {
        res = matrix.multiple(res).multiple(res);
        n = (n - 1) / 2;
      }
    }
    return res;
  }
}


const fabonacci = (n: number) => {
  if(n < 2) return 1;
  const base = new Matrix(1, 2);
  base.set([
    [1, 1]
  ]);
  const matrix = new Matrix(2, 2);
  matrix.set([
    [1, 1],
    [1, 0]
  ])
  const res = base.multiple(matrix.fastPow(n - 1));
  return res.value[0][0];
}

for(let i = 0; i < 100; i++) {
  console.log(
    fabonacci(i)
  )
}