优先队列

1. 什么是优先队列

队列与优先队列
优先队列是一种特殊的队列，只不过不同的是优先队列出队的顺序是由元素的优先级决定的。

元素优先级最高或者优先级最低的元素优先出队。

优先队列比较常用的是使用堆来实现。

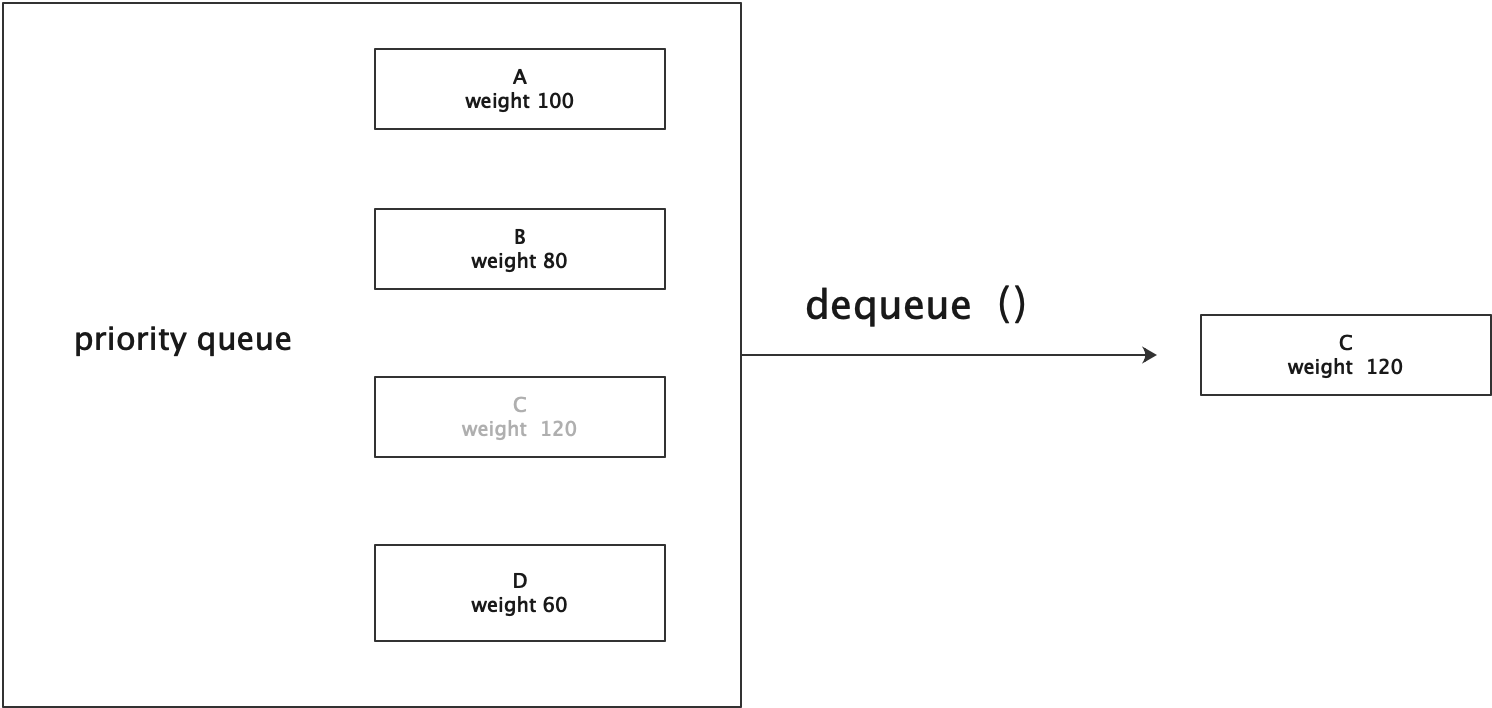
在一个优先队列中，有若干个不同权重的事务，权重值最高的元素优先被取出
优先队列支持的操作
入队(enqueue)：插入一个带有优先级的元素

出队(dequeue)：从队列中取出优先级最高的元素

查看(top)：查看队列中优先级最高的元素

调整(update)：更新队列中某元素的优先级
优先队列至少需要支持下述操作：
- 插入带优先级的元素（insert_with_priority）
- 取出具有最高优先级的元素（pull_highest_priority_element）
- 查看最高优先级的元素（peek）：O(1) 时间复杂度
其它可选的操作：
- 检查优先级高的一批元素
- 清空优先队列
- 批插入一批元素
- 合并多个优先队列
- 调整一个元素的优先级

2. 优先队列的实现方法

数组
二叉堆
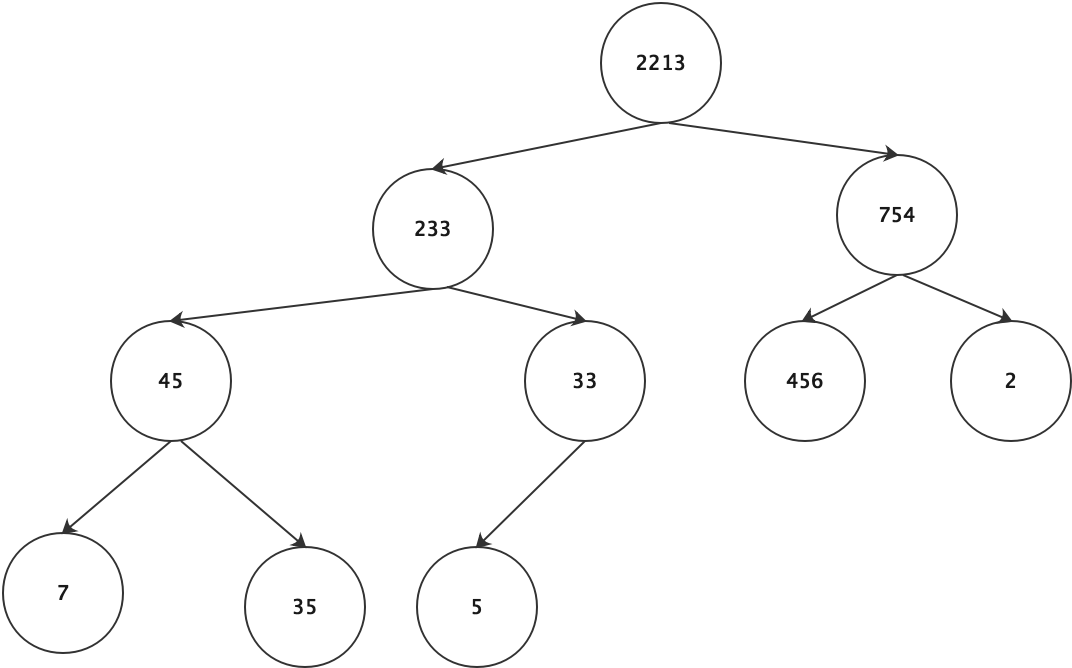
二叉搜索树

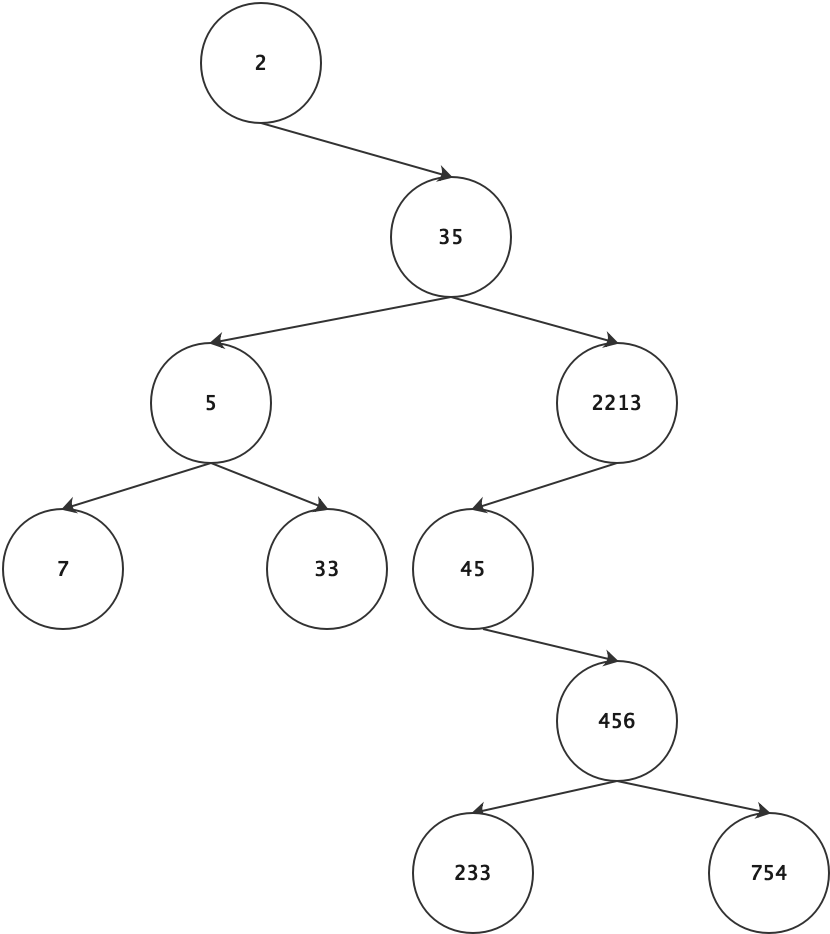
(其实说二叉搜索树的复杂度为O(log n)并不是特别准确，因为二叉搜索树的构造受到数据的影响，生成的二叉搜索树不一定是最优的，只有在二叉搜索树平衡的情况下，才可以说复杂度为O(log n))

	数组	二叉堆	二叉搜索树
enqueue	O(1)	O(log n)	O(log n)
dequeue	O(n)	O(log n)	O(log n)
top	O(n)	O(1)	O(log n)
update	O(n)	O(n)	O(log n)

3. 用堆来实现优先队列

堆（Heap)

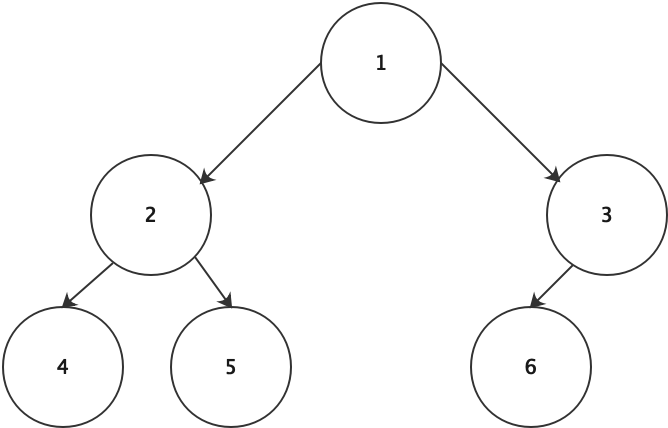
堆（英语：Heap）是计算机科学中的一种特别的完全二叉树。若是满足以下特性，即可称为堆：“给定堆中任意节点P和C，若P是C的母节点，那么P的值会小于等于（或大于等于）C的值”。若母节点的值恒小于等于子节点的值，此堆称为最小堆（min heap）；反之，若母节点的值恒大于等于子节点的值，此堆称为最大堆（max heap）。在堆中最顶端的那一个节点，称作根节点（root node），根节点本身没有母节点（parent node）。

堆是一种特别的完全二叉树

最大堆：父节点的权重值比器左右子节点的权重值要大

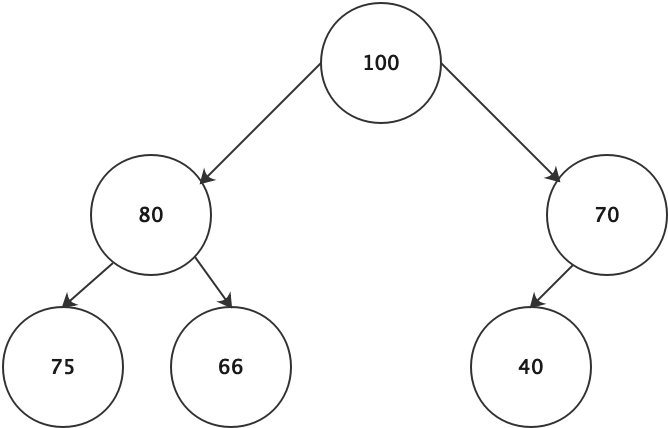
最小堆：父节点的权重值始终比左右子节点的权重值要小
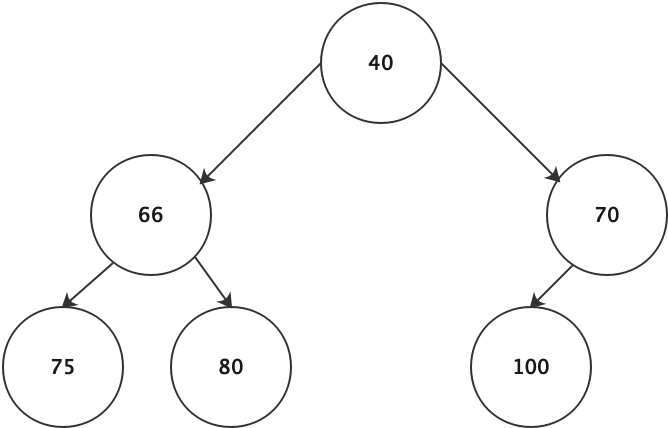
堆的逻辑结构是一颗完全二叉树，存储结构是一个一维数组

完全二叉树具备的性质：
1. 具有n个元素的二叉堆，高度为 log(n)
2. 叶子节点数量
  
  对于有n个节点的二叉堆
  
  如果n为奇数，叶子结点数为 Math.ceil(n / 2);
  
  如果n为偶数，叶子结点数为n/2;
3. 若二叉堆存储的数组下标从1开始
  
  下标为 i 的元素，左子节点的下标为 i * 2，右子节点的下标为 i * 2 + 1

堆的操作（以最大堆为例，最小堆类似）

shiftDown 堆化函数

shiftDown函数用于维护最大堆的性质，假定有一个堆heap[i],对于heap[i]来说，其左右子堆heap[ 2 * i], heap[ 2 * i + 1]均满足最大堆性质，
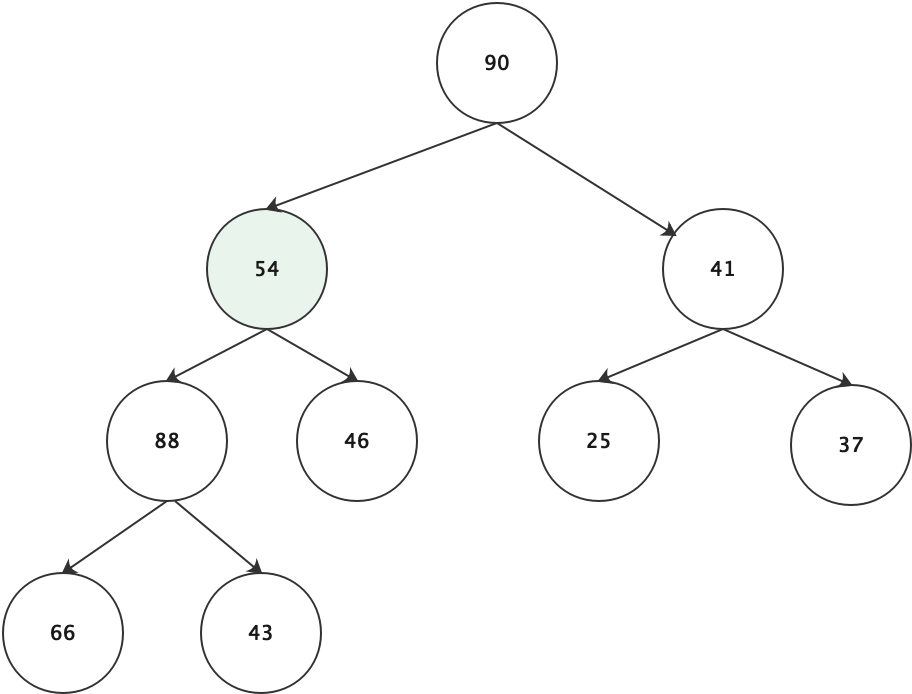
shiftUp函数

shiftUp函数往往用于向最大堆中末尾插入一个元素时，插入的元素可能破坏了最大堆的性质，需要进行上浮操作，以维持堆的特性
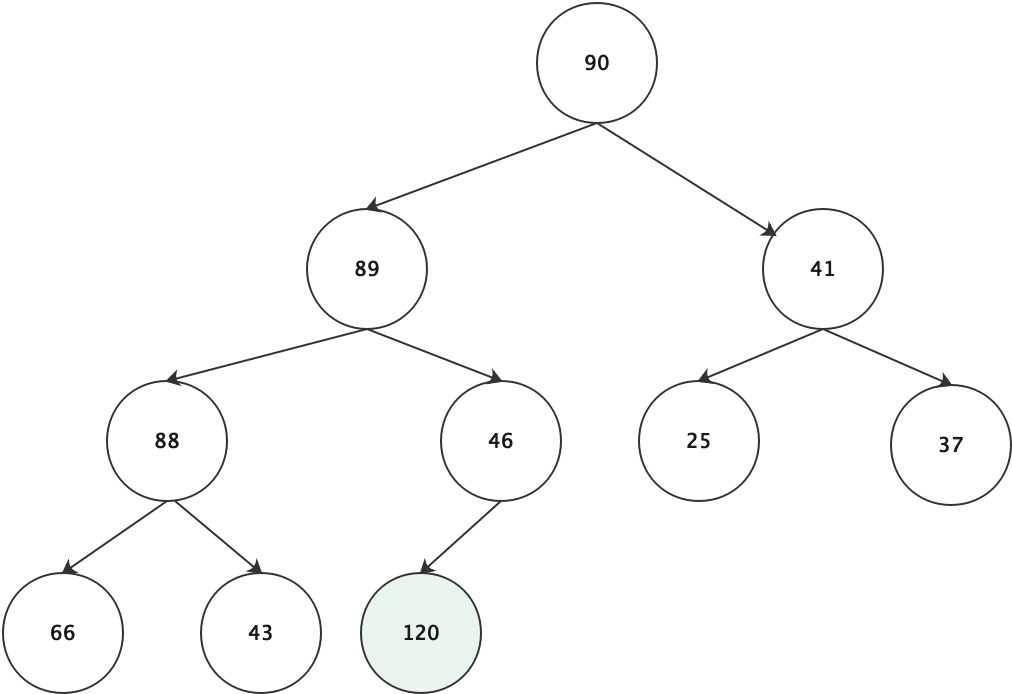
build：构造一个大顶堆
heapSort：堆排序

export interface IComparable {
  key: number;
}

class MaxHeap<ABT extends IComparable> {

  protected _heap: ABT[];

  constructor(list: ABT[]) {
    // 构造时下标从1开始，方便计算
    this._heap = [null, ...list];
    this.build();
  }

  get data(): ABT[] {
    return this._heap.slice(1);
  }

  public static left(parentIndex: number) {
    return parentIndex * 2;
  }

  public static right(parentIndex: number) {
    return parentIndex * 2 + 1;
  }

  public static parent(childIndex: number) {
    return Math.floor(childIndex / 2);
  }

  protected swap(i: number, j: number) {
    const _heap = this._heap;
    if (i < 1 || j >= _heap.length)
      throw new Error('Exception: out of boundary...');
    const _tmep = _heap[i];
    _heap[i] = _heap[j];
    _heap[j] = _tmep;
  }

  public shiftDown (index: number) {
    const _heap = this._heap;
    const pIndex = index;
    const lIndex = MaxHeap.left(index);
    const rIndex = MaxHeap.right(index);
    let maxIndex: number = pIndex;
    [lIndex, rIndex].forEach(idx => {
      if (!_heap[maxIndex] || !_heap[idx]) return;
      if (_heap[maxIndex].key < _heap[idx].key) maxIndex = idx;
    });
    if (maxIndex === pIndex) return;
    this.swap(maxIndex, pIndex);
    this.shiftDown(maxIndex);
  }

  public shiftUp(childIndex: number) {
    const _heap = this._heap;
    while(childIndex > 1 && _heap[childIndex].key > _heap[MaxHeap.parent(childIndex)].key) {
      this.swap(childIndex, MaxHeap.parent(childIndex));
      childIndex = MaxHeap.parent(childIndex);
    }
  }

  /**
   * 构建一个大顶堆
   */
  public build () {
    const _heap = this._heap;
    for (let i = Math.floor(_heap.length / 2); i > 0; i--) {
      this.shiftDown(i);
    }
  }

  /**
   * 查询当前权重最大的元素
   */
  public top (): ABT {
    if (this._heap.length <= 1) return null;
    return this._heap[1];
  }

  public empty(): boolean {
    return this._heap.length <= 1;
  }
}

优先队列

import MaxHeap from './Heap';
import { IComparable } from './Heap';
class PriorityQueue<ADT extends IComparable> extends MaxHeap<ADT> {
  constructor(list: ADT[]) {
    super(list);
  }

  public enqueue(item: ADT) {
    this._heap.push(item);
    this.shiftUp(this._heap.length - 1);
  }

  public dequeue(): ADT {
    if (this.empty()) return null;
    if (this._heap.length === 2) return this._heap.pop();
    const _top = this._heap[1];
    this._heap[1] = this._heap.pop();
    this.shiftDown(1);
    return _top;
  }

  public update(oldKey, newKey): boolean{
    if (this.empty()) return false;
    const _heap = this._heap;
    let targetIndex = this._heap
      .filter(item => item !== null)
      .findIndex(
        item => item.key === oldKey
      )
    if (targetIndex === -1) return false;
    targetIndex++;
    _heap[targetIndex].key = newKey;
    if (newKey < oldKey) {
      this.shiftDown(targetIndex);
      return true;
    } else {
      this.shiftUp(targetIndex);
      return true;
    }
  }

}

优先队列

1. 什么是优先队列

队列与优先队列

优先队列支持的操作

2. 优先队列的实现方法

数组

二叉堆

二叉搜索树

3. 用堆来实现优先队列

堆（Heap)

堆的操作（以最大堆为例，最小堆类似）